常用积分表
必背
( 1 ) ∫ k d x = k x + C ( 2 ) ∫ x a d x = x a + 1 a + 1 + C ( 3 ) ∫ 1 x d x = ln ∣ x ∣ + C ( 4 ) ∫ 1 1 + x 2 d x = arctan x + C ( 5 ) ∫ 1 1 − x 2 d x = arcsin x + C ( 6 ) ∫ a x d x = 1 ln a a x + C ( 7 ) ∫ cos x d x = sin x + C ( 8 ) ∫ sin x d x = − cos x + C ( 9 ) ∫ sec 2 x d x = tan x + C ( 10 ) ∫ csc 2 x d x = − cot x + C ( 11 ) ∫ sec x tan x d x = sec x + C ( 12 ) ∫ csc x cot x d x = − csc x + C ( 13 ) ∫ sec x d x = ln ∣ sec x + tan x ∣ + C ( 14 ) ∫ csc x d x = ln ∣ csc x − cot x ∣ + C \begin{array}{}
(1) \int kdx = kx +C & (2) \int x^adx = \frac{x^{a+1}}{a+1}+C\\
(3) \int{\frac{1}{x}}dx = \ln|x|+C& (4) \int \frac{1}{1+x^2}dx = \arctan x+C \\
(5)\int{\frac{1}{\sqrt{ 1-x^2 }}dx}=\arcsin x+C & (6)\int a^xdx=\frac{1}{\ln a}a^x+C \\
(7)\int \cos xdx = \sin x+C & (8)\int \sin xdx= -\cos x+C \\
(9)\int \sec^2xdx= \tan x+C & (10)\int \csc^2xdx=-\cot x+C \\
(11)\int \sec x\tan xdx=\sec x+C&(12)\int \csc x\cot xdx=-\csc x+C \\
(13)\int \sec xdx=\ln|\sec x+\tan x|+C&(14)\int \csc xdx=\ln|\csc x-\cot x|+C
\end{array} ( 1 ) ∫ k d x = k x + C ( 3 ) ∫ x 1 d x = ln ∣ x ∣ + C ( 5 ) ∫ 1 − x 2 1 d x = arcsin x + C ( 7 ) ∫ cos x d x = sin x + C ( 9 ) ∫ sec 2 x d x = tan x + C ( 11 ) ∫ sec x tan x d x = sec x + C ( 13 ) ∫ sec x d x = ln ∣ sec x + tan x ∣ + C ( 2 ) ∫ x a d x = a + 1 x a + 1 + C ( 4 ) ∫ 1 + x 2 1 d x = arctan x + C ( 6 ) ∫ a x d x = l n a 1 a x + C ( 8 ) ∫ sin x d x = − cos x + C ( 10 ) ∫ csc 2 x d x = − cot x + C ( 12 ) ∫ csc x cot x d x = − csc x + C ( 14 ) ∫ csc x d x = ln ∣ csc x − cot x ∣ + C 考前必背
( 1 ) ∫ tan x d x = − ln ∣ cos x ∣ + C ( 2 ) ∫ cot x d x = ln ∣ sin x ∣ + C ( 3 ) ∫ d x x 2 + a 2 = 1 a arctan ( x a ) + C ( 4 ) ∫ d x x 2 ± a 2 = ln ∣ x + x 2 ± a 2 ∣ + C ( 5 ) ∫ d x a 2 − x 2 = arcsin ( x a ) + C ( 6 ) ∫ d x a 2 − x 2 = 1 2 a ln ∣ a + x a − x ∣ + C \begin{array}{ll}
(1)\,\int \tan x\,dx = -\ln|\cos x| + C
& (2)\,\int \cot x\,dx = \ln|\sin x| + C \\
(3)\,\int \frac{dx}{x^2 + a^2} = \frac{1}{a}\arctan\!\Bigl(\frac{x}{a}\Bigr) + C
& (4)\,\int \frac{dx}{\sqrt{x^2 \pm a^2}} = \ln\!\bigl|\,x + \sqrt{x^2 \pm a^2}\,\bigr| + C \\
(5)\,\int \frac{dx}{\sqrt{a^2 - x^2}} = \arcsin\!\Bigl(\frac{x}{a}\Bigr) + C
& (6)\,\int \frac{dx}{a^2 - x^2} = \frac{1}{2a}\ln\!\Bigl|\frac{\,a + x\,}{\,a - x\,}\Bigr| + C
\end{array} ( 1 ) ∫ tan x d x = − ln ∣ cos x ∣ + C ( 3 ) ∫ x 2 + a 2 d x = a 1 arctan ( a x ) + C ( 5 ) ∫ a 2 − x 2 d x = arcsin ( a x ) + C ( 2 ) ∫ cot x d x = ln ∣ sin x ∣ + C ( 4 ) ∫ x 2 ± a 2 d x = ln x + x 2 ± a 2 + C ( 6 ) ∫ a 2 − x 2 d x = 2 a 1 ln a − x a + x + C 例题
例一 ∫ 1 x 4 ( x 2 + 1 ) d x \int\frac{{1}}{x^4(x^2+1)}dx ∫ x 4 ( x 2 + 1 ) 1 d x
[!NOTE] 关键点
通过分项的方法:抄分母,加一个,减一个。
原式 = ∫ ( 1 + x 2 ) − x 2 x 4 ( x 2 + 1 ) d x = ∫ 1 x 4 d x − ∫ 1 x 2 ( x 2 + 1 ) d x = ∫ 1 x 4 d x − ∫ 1 + x 2 − x 2 x 2 ( x 2 + 1 ) d x = ∫ 1 x 4 d x − ∫ 1 x 2 d x + ∫ 1 x 2 + 1 d x = − 1 3 x − 3 − 1 x + arctan x + C \begin{aligned}
\text{原式}=\int\frac{{(1+x^2)-x^2}}{x^4(x^2+1)}dx&=\int \frac{1}{x^4}dx-\int \frac{1}{x^2(x^2+1)}dx\\
&=\int\frac{{1}}{x^4}dx-\int{\frac{{1+x^2-x^2}}{x^2(x^2+1)}}dx\\
&=\int \frac{1}{x^4}dx-\int \frac{1}{x^2}dx+\int \frac{1}{x^2+1}dx\\
&=-\frac{1}{3}x^{-3}-\frac{1}{x}+\arctan x+C
\end{aligned} 原式 = ∫ x 4 ( x 2 + 1 ) ( 1 + x 2 ) − x 2 d x = ∫ x 4 1 d x − ∫ x 2 ( x 2 + 1 ) 1 d x = ∫ x 4 1 d x − ∫ x 2 ( x 2 + 1 ) 1 + x 2 − x 2 d x = ∫ x 4 1 d x − ∫ x 2 1 d x + ∫ x 2 + 1 1 d x = − 3 1 x − 3 − x 1 + arctan x + C 例二 ∫ tan 2 x d x \int \tan^2xdx ∫ tan 2 x d x
[!NOTE] 关键点
tan 2 x + 1 = sec 2 x \tan^2x+1=\sec^2x tan 2 x + 1 = sec 2 x sin 2 x + cos 2 x = 1 \sin^2x+\cos^2x=1 sin 2 x + cos 2 x = 1 cos 2 x \cos^2x cos 2 x
原式 = ∫ ( sec 2 − 1 ) d x = tan x − x + C \begin{align}
\text{原式} &=\int(\sec^2-1)dx\\ \\
&=\tan x-x+C
\end{align} 原式 = ∫ ( sec 2 − 1 ) d x = tan x − x + C 例三 ∫ cos 2 x 2 d x \int \cos^2{\frac{x}{2}}dx ∫ cos 2 2 x d x
[!NOTE] 关键点:三角恒等变换
sin α cos α = 1 2 sin 2 α \sin\alpha \cos\alpha=\frac{1}{2}\sin2\alpha sin α cos α = 2 1 sin 2 α cos 2 α = 1 + cos 2 α 2 \cos^2\alpha=\frac{{1+\cos 2\alpha}}{2} cos 2 α = 2 1 + c o s 2 α sin 2 α = 1 − cos 2 α 2 \sin^2\alpha=\frac{{1-\cos2\alpha}}{2} sin 2 α = 2 1 − c o s 2 α
原式 = ∫ 1 + cos x 2 d x = ∫ 1 2 d x + ∫ cos x 2 d x = 1 2 x + 1 2 sin x + C \begin{align}
\text{原式}&=\int{\frac{{1+\cos x}}{2}}dx \\
&=\int \frac{1}{2}dx+\int \frac{{\cos x}}{2}dx \\
&=\frac{1}{2}x+\frac{1}{2}\sin x+C
\end{align} 原式 = ∫ 2 1 + cos x d x = ∫ 2 1 d x + ∫ 2 cos x d x = 2 1 x + 2 1 sin x + C 常用凑微分公式
∫ f ( a x + b ) d x = 1 a ∫ f ( a x + b ) d ( a x + b ) ( a ≠ 0 ) ∫ f ( sin x ) cos x d x = ∫ f ( sin x ) d ( sin x ) ∫ f ( ln x ) 1 x d x = ∫ f ( ln x ) d ( ln x ) ∫ f ( x ) d x x = 2 ∫ f ( x ) d ( x ) ∫ f ( arctan x ) d x 1 + x 2 = ∫ f ( arctan x ) d ( arctan x ) \begin{array}{l}
\int f(ax+b)\,dx = \frac{1}{a}\int f(ax+b)\,d(ax+b)\quad (a\neq0)\\[6pt]
\int f(\sin x)\cos x\,dx = \int f(\sin x)\,d(\sin x)\\[6pt]
\int f(\ln x)\frac{1}{x}\,dx = \int f(\ln x)\,d(\ln x)\\[6pt]
\int f\bigl(\sqrt{x}\bigr)\frac{dx}{\sqrt{x}} = 2\int f\bigl(\sqrt{x}\bigr)\,d\bigl(\sqrt{x}\bigr)\\[6pt]
\int f(\arctan x)\frac{dx}{1+x^2} = \int f(\arctan x)\,d(\arctan x)
\end{array} ∫ f ( a x + b ) d x = a 1 ∫ f ( a x + b ) d ( a x + b ) ( a = 0 ) ∫ f ( sin x ) cos x d x = ∫ f ( sin x ) d ( sin x ) ∫ f ( ln x ) x 1 d x = ∫ f ( ln x ) d ( ln x ) ∫ f ( x ) x d x = 2 ∫ f ( x ) d ( x ) ∫ f ( arctan x ) 1 + x 2 d x = ∫ f ( arctan x ) d ( arctan x ) 例题
例四 ∫ cos ( e x ) e x d x \int \cos (e^x)e^xdx ∫ cos ( e x ) e x d x
[!NOTE] 关键点:第一类换元积分法
∫ f [ φ ( x ) ] φ ′ ( x ) d x = ( ∫ f ( u ) d u ) u = φ ( x ) \int f \left[ \varphi (x) \right] \varphi' (x) \, dx = \left ( \int f (u) \, du \right)_{u = \varphi (x)} ∫ f [ φ ( x ) ] φ ′ ( x ) d x = ( ∫ f ( u ) d u ) u = φ ( x )
d f ( x ) = f ′ ( x ) d x → d e x = e x d x df(x)=f'(x)dx\to de^x=e^xdx df ( x ) = f ′ ( x ) d x → d e x = e x d x e x e^x e x u u u
原式 = ∫ cos e x d e x = sin e x + C \begin{align}
\text{原式}&=\int \cos e^xde^x \\
&=\sin e^x +C
\end{align} 原式 = ∫ cos e x d e x = sin e x + C 例五 ∫ tan x d x \int \tan xdx ∫ tan x d x
原式 = ∫ sin x cos x d x = − ∫ 1 cos x d cos x = − ln ∣ cos x ∣ + C \begin{align}
\text{原式}&=\int \frac{{\sin x}}{\cos x}dx \\
&=-\int \frac{1}{\cos x}d\cos x \\
&=-\ln|\cos x|+C
\end{align} 原式 = ∫ cos x sin x d x = − ∫ cos x 1 d cos x = − ln ∣ cos x ∣ + C 例六 ∫ 1 a 2 − x 2 d x \int \frac{{1}}{\sqrt{ a^2-x^2 }}dx ∫ a 2 − x 2 1 d x
原式 = ∫ 1 a 2 ( 1 − ( x a ) 2 ) d x = ∫ 1 1 − ( x a ) 2 ⋅ 1 a d x = ∫ 1 1 + ( x a ) 2 d x a = arcsin x a + C \begin{align}
\text{原式}&=\int{\frac{{1}}{\sqrt{ a^2\left( 1-\left( \frac{x}{a} \right)^2 \right) }}}dx \\
&=\int {\frac{{1}}{\sqrt{ 1-\left( \frac{x}{a} \right)^2 }}}{\cdot\frac{{1}}{a}}dx \\
&=\int {\frac{{1}}{\sqrt{ 1+\left( \frac{x}{a} \right)^2 }}}d{\frac{x}{a}} \\
&=\arcsin{\frac{x}{a}}+C
\end{align} 原式 = ∫ a 2 ( 1 − ( a x ) 2 ) 1 d x = ∫ 1 − ( a x ) 2 1 ⋅ a 1 d x = ∫ 1 + ( a x ) 2 1 d a x = arcsin a x + C 例七 ∫ d x x ( 1 + x ) \int \frac{{dx}}{\sqrt{ x }(1+x)} ∫ x ( 1 + x ) d x
[!NOTE] 关键点
d x = ( x ) ′ d x = 1 2 x d x d\sqrt{ x }=(\sqrt{ x })'dx=\frac{{1}}{2\sqrt{ x }}dx d x = ( x ) ′ d x = 2 x 1 d x d x x = 2 d x {\frac{dx}{\sqrt{ x }}=2d\sqrt{ x }} x d x = 2 d x
原式 = 2 ∫ 1 1 + ( x ) 2 d x = 2 arctan x \begin{align}
\text{原式}&=2\int \frac{{1}}{1+(\sqrt{ x })^2}d\sqrt{ x } \\
&=2\arctan \sqrt{ x }
\end{align} 原式 = 2 ∫ 1 + ( x ) 2 1 d x = 2 arctan x 常见换元法
[!NOTE] 第二类换元积分法
∫ f ( x ) d x = ( ∫ f [ φ ( t ) ] φ ′ ( t ) d t ) t = φ − 1 ( x ) \int f (x) \, dx = \left ( \int f \left[ \varphi (t) \right] \varphi'(t) \, dt \right)_{t = \varphi^{-1}(x)} ∫ f ( x ) d x = ( ∫ f [ φ ( t ) ] φ ′ ( t ) d t ) t = φ − 1 ( x )
三角代换
被积函数含 a 2 − x 2 ( a > 0 ) \sqrt{ a^2-x^2 }(a>0) a 2 − x 2 ( a > 0 ) x = a sin t , t ∈ [ − π 2 , π 2 ] x=a\sin t,t \in\left[ {-\frac{\pi}{2},{\frac{\pi}{2}}} \right] x = a sin t , t ∈ [ − 2 π , 2 π ] a 2 − x 2 = a cos t \sqrt{ a^2-x^2 }=a\cos t a 2 − x 2 = a cos t x 2 + a 2 ( a > 0 ) \sqrt{ x^2+a^2 }(a>0) x 2 + a 2 ( a > 0 ) x = a tan t , t ∈ [ − π 2 , π 2 ] x=a\tan t,t \in\left[ {-\frac{\pi}{2},{\frac{\pi}{2}}} \right] x = a tan t , t ∈ [ − 2 π , 2 π ] x 2 + a 2 = a sec t \sqrt{ x^2+a^2 }=a\sec t x 2 + a 2 = a sec t x 2 − a 2 ( a > 0 ) \sqrt{ x^2-a^2 }(a>0) x 2 − a 2 ( a > 0 ) x = a sec t , t ∈ [ 0 , π 2 ) ∪ ( π 2 , π ] x=a\sec t,t \in\left[ {0},{\frac{\pi}{2}})\cup({\frac{\pi}{2},\pi} \right] x = a sec t , t ∈ [ 0 , 2 π ) ∪ ( 2 π , π ] x 2 − a 2 = a tan t \sqrt{ x^2-a^2 }=a\tan t x 2 − a 2 = a tan t
根式代换
见例八
例题
例八 ∫ d x 1 + x \int \frac{dx}{{1+\sqrt{ x }}} ∫ 1 + x d x
[!NOTE] 关键点:根式代换
令 t = x 原式 = ∫ d t 2 1 + t = ∫ 2 t d t 1 + t = 2 ∫ ( t + 1 ) − 1 t + 1 d t = 2 [ ∫ d t − ∫ 1 1 + t d t ] = 2 [ t − ln ( t + 1 ) ] + C = 2 x ⋅ 2 ln ( x + 1 ) + C \begin{align}
\text{令}t=\sqrt{ x } \\
\text{原式}&=\int {\frac{{dt^2}}{1+t}} \\
&=\int {\frac{{2tdt}}{1+t}}=2\int {\frac{{(t+1)-1}}{t+1}}dt \\
&=2\left[ \int dt-\int \frac{1}{1+t}dt \right] \\
&=2[t-\ln (t+1)]+C \\
&=2\sqrt{ x }\cdot 2\ln(\sqrt{ x }+1)+C
\end{align} 令 t = x 原式 = ∫ 1 + t d t 2 = ∫ 1 + t 2 t d t = 2 ∫ t + 1 ( t + 1 ) − 1 d t = 2 [ ∫ d t − ∫ 1 + t 1 d t ] = 2 [ t − ln ( t + 1 )] + C = 2 x ⋅ 2 ln ( x + 1 ) + C 例九 ∫ a 2 − x 2 d x \int \sqrt{ a^2-x^2 }dx ∫ a 2 − x 2 d x
[!NOTE] 关键点:三角代换
利用图形将新元替换为旧元
令 x = a sin t 原式 = ∫ a cos t ⋅ a cos t d t = ∫ a 2 cos 2 t d t = a 2 ∫ cos 2 t d t = a 2 2 ∫ ( 1 + cos 2 t ) d t = a 2 2 ( ∫ d t + 1 2 ∫ cos 2 t d 2 t ) = a 2 2 t + a 2 4 sin 2 t + C \begin{align}
\text{令}x=a\sin t \\
\text{原式}&=\int a\cos t\cdot a\cos tdt \\
&=\int a^2\cos^2tdt=a^2\int \cos^2tdt=\frac{a^2}{2}\int(1+\cos 2t)dt \\
&=\frac{a^2}{2}\left( \int dt + \frac{1}{2}\int \cos 2t d 2t\right) \\
&=\frac{a^2}{2}t+\frac{a^2}{4}\sin 2t+C
\end{align} 令 x = a sin t 原式 = ∫ a cos t ⋅ a cos t d t = ∫ a 2 cos 2 t d t = a 2 ∫ cos 2 t d t = 2 a 2 ∫ ( 1 + cos 2 t ) d t = 2 a 2 ( ∫ d t + 2 1 ∫ cos 2 t d 2 t ) = 2 a 2 t + 4 a 2 sin 2 t + C
原式 = a 2 2 arcsin x a + a 2 2 ⋅ x a ⋅ a 2 − x 2 a + C = a 2 2 arcsin x a + x a a 2 − x 2 + C \begin{align}
\text{原式}&=\frac{a^2}{2}\arcsin \frac{{x}}{a} +\frac{a^2}{2}\cdot \frac{x}{a}\cdot{\frac{\sqrt{ a^2-x^2 }}{a}}+C \\
&=\frac{a^2}{2}\arcsin \frac{x}{a}+\frac{x}{a}\sqrt{ a^2-x^2 }+C
\end{align} 原式 = 2 a 2 arcsin a x + 2 a 2 ⋅ a x ⋅ a a 2 − x 2 + C = 2 a 2 arcsin a x + a x a 2 − x 2 + C 分部积分法
∫ u ( x ) d v ( x ) = u ( x ) v ( x ) − ∫ v ( x ) d u ( x ) \begin{align}
\int u(x)dv(x)=u(x)v(x)-\int v(x)du(x)
\end{align} ∫ u ( x ) d v ( x ) = u ( x ) v ( x ) − ∫ v ( x ) d u ( x )
[!NOTE] 技巧
一般可依次选择 u 的顺序为:反三角函数,对数函数,幂函数,指数函数。三角函数 (反对幂指三)
例题
例十 ∫ x 2 ln x d x \int x^2\ln xdx ∫ x 2 ln x d x
[!NOTE] 技巧
灵活结合换元法
原式 = ∫ ln x x 2 d x = 1 3 ∫ ln x d x 3 = 1 3 ( ln x ⋅ x 3 − ∫ x 3 d ln x ) = 1 3 ( x 3 ln x − ∫ x 2 d x ) = 1 3 ( x 3 ln x − 1 3 x 3 ) + C \begin{align}
\text{原式}&=\int \ln x x^2dx=\frac{1}{3}\int \ln x dx^3 \\
&=\frac{1}{3}\left( \ln x\cdot x^3-\int x^3d\ln x \right) \\
&=\frac{1}{3}\left( x^3\ln x-\int x^2dx \right) \\
&=\frac{1}{3}\left( x^3\ln x-\frac{1}{3}x^3 \right)+C
\end{align} 原式 = ∫ ln x x 2 d x = 3 1 ∫ ln x d x 3 = 3 1 ( ln x ⋅ x 3 − ∫ x 3 d ln x ) = 3 1 ( x 3 ln x − ∫ x 2 d x ) = 3 1 ( x 3 ln x − 3 1 x 3 ) + C 例十一 ∫ x e x ( x + 1 ) 2 d x \int {\frac{{xe^x}}{(x+1)^2}}dx ∫ ( x + 1 ) 2 x e x d x
[!NOTE] 关键
∫ e x ( x + 1 ) 2 d x = ∫ e x ( x + 1 ) 2 d ( x + 1 ) \int \frac{e^x}{(x+1)^2}dx=\int \frac{e^x}{(x+1)^2}d(x+1) ∫ ( x + 1 ) 2 e x d x = ∫ ( x + 1 ) 2 e x d ( x + 1 )
原式 = ∫ ( x + 1 ) − 1 ( x + 1 ) 2 ⋅ e x d x = ∫ e x x + 1 d x − ∫ e x ( x + 1 ) 2 d x = ∫ e x x + 1 d x + ∫ e x d 1 x + 1 = ∫ e x x + 1 d x + e x ⋅ 1 x + 1 − ∫ e x x + 1 d x = e x x + 1 + C \begin{align}
\text{原式}&=\int {\frac{{(x+1)-1}}{(x+1)^2}}\cdot e^xdx=\int \frac{e^x}{x+1}dx-\int \frac{e^x}{(x+1)^2}dx \\
&=\int \frac{e^x}{x+1}dx+\int e^xd \frac{{1}}{x+1} \\
&=\int \frac{e^x}{x+1}dx+e^x\cdot \frac{{1}}{x+1}-\int \frac{e^x}{x+1}dx \\
&=\frac{e^x}{x+1}+C
\end{align} 原式 = ∫ ( x + 1 ) 2 ( x + 1 ) − 1 ⋅ e x d x = ∫ x + 1 e x d x − ∫ ( x + 1 ) 2 e x d x = ∫ x + 1 e x d x + ∫ e x d x + 1 1 = ∫ x + 1 e x d x + e x ⋅ x + 1 1 − ∫ x + 1 e x d x = x + 1 e x + C 含 sin m x ⋅ cos n x \sin^mx\cdot \cos^nx sin m x ⋅ cos n x
sin x 奇次, cos x 偶次 → d ( cos x ) 或 d ( sin x ) cos x 奇次, sin x 偶次 → d ( sin x ) 或 d ( cos x ) cos x 和 sin x 同为偶次或奇次 → d ( tan x ) 或 d ( cos x ) \begin{align}
\sin x \text{奇次,}\cos x \text{偶次} \rightarrow d(\cos x) \text{ 或 } d(\sin x)\\
\cos x \text{奇次,}\sin x \text{偶次} \rightarrow d(\sin x) \text{ 或 } d(\cos x)\\
\cos x \text{和}\sin x \text{同为偶次或奇次} \rightarrow d(\tan x) \text{ 或 } d(\cos x)
\end{align} sin x 奇次, cos x 偶次 → d ( cos x ) 或 d ( sin x ) cos x 奇次, sin x 偶次 → d ( sin x ) 或 d ( cos x ) cos x 和 sin x 同为偶次或奇次 → d ( tan x ) 或 d ( cos x ) 例题
例十二 ∫ 1 sin 3 x ⋅ cos x d x \int \frac{1}{\sin^3x\cdot \cos x}dx ∫ s i n 3 x ⋅ c o s x 1 d x
[!NOTE] 关键点
将 sec 4 x \sec^4x sec 4 x sec 2 x ⋅ sec 2 x \sec^2x\cdot \sec^2x sec 2 x ⋅ sec 2 x sec 2 x \sec^2x sec 2 x d x dx d x
上下同时除以 cos 4 x 原式 = ∫ sec 4 x tan 3 x d x = ∫ ( tan 2 x + 1 ) d tan x tan 3 x = ∫ ( 1 tan x + tan − 3 x ) d tan x = ln ∣ tan x ∣ − 1 2 tan − 2 x + C \begin{align}
\text{上下同时除以}\cos^4x \\
\text{原式}&=\int \frac{\sec^4x}{\tan^3x}dx \\
&=\int {\frac{{(\tan^2x+1)d\tan x}}{\tan^3x}}=\int \left( {\frac{1}{\tan x}+\tan^{-3}x} \right)d\tan x \\
&=\ln|\tan x|-\frac{1}{2}\tan^{-2}x+C
\end{align} 上下同时除以 cos 4 x 原式 = ∫ tan 3 x sec 4 x d x = ∫ tan 3 x ( tan 2 x + 1 ) d tan x = ∫ ( tan x 1 + tan − 3 x ) d tan x = ln ∣ tan x ∣ − 2 1 tan − 2 x + C 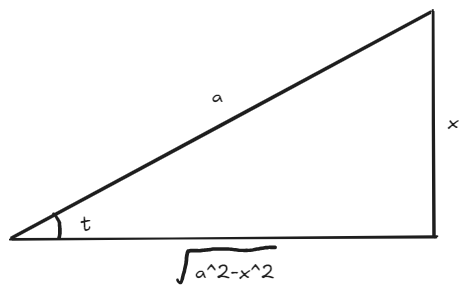 所以
所以